Linearithmic sorts are optimal!
- Justify $\Omega(n \lg n)$ is the lower bound for comparison-based sorting algorithms.
Let's restate the observation made earlier:
Since the decision tree is a binary tree, its height is at least $\lg N$ where $N$ is the number of nodes. Therefore, the lower bound on any comparison-based algorithm modeled by this decision tree is $\Omega(\lg N)$.
For sorting, $N$ is $\Omicron(n!)$ where $n$ is the number of elements in the collection to be sorted.
Why?
In the decision tree corresponding to the comparison-based sorting algorithm, the number of leaves is greater or equal to the number of possible answers which is greater or equal to $n!$, the number of permutations of the elements.
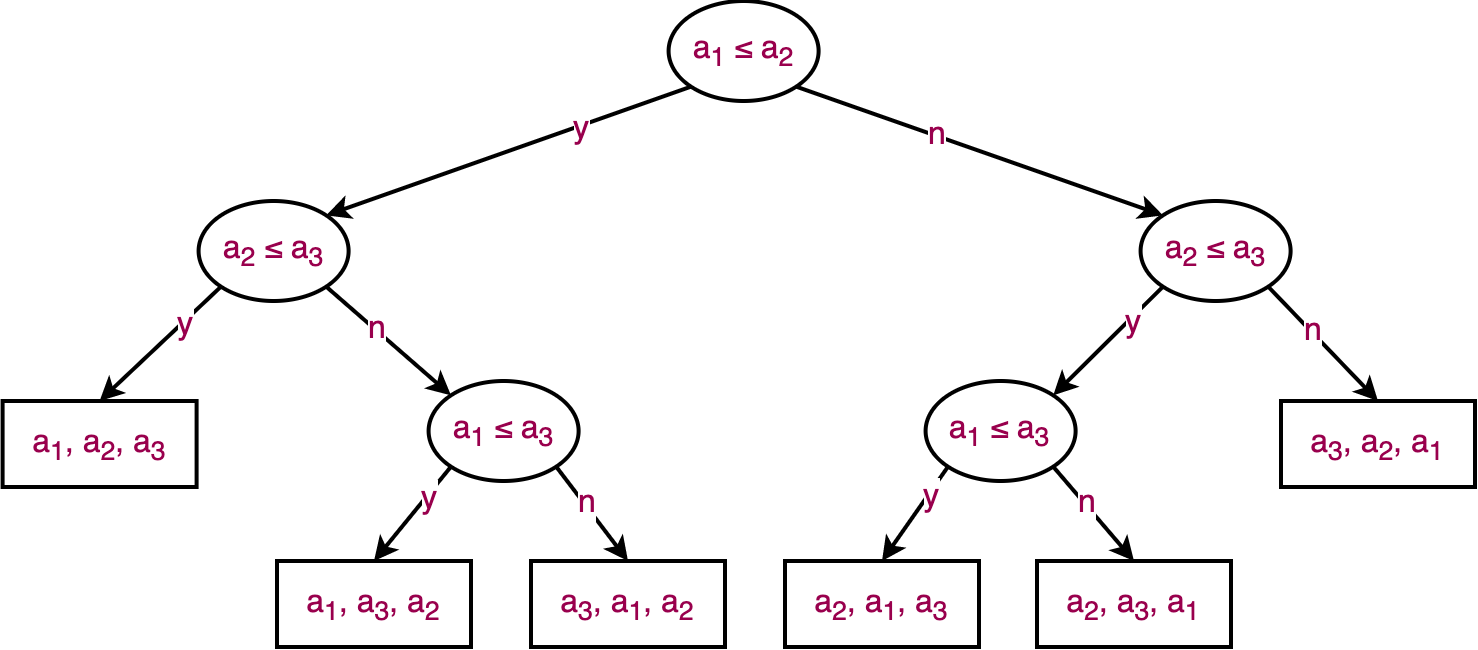
As it can be seen in the diagram above, for a collection with $3$ elements, there are $3!=6$ permutations in which one is the correct answer (elements in sorted order; there is only one sorted order if elements are unique).
So, if there are at least $n!$ leaves, there are at least $2(n!)$ nodes. The height of the tree, therefore, is at least $\lg 2(n!)$.
Therefore, the lower bound on any comparison-based sorting algorithm is $\Omega(\lg n!)$ where $n$ is the size of the collection.
We can show $\Omega(\lg n!) \in \Omega(n \lg n)$. In other words, linearithmic sorts are optimal!
How come?
Expand $n!$
$$ \lg n! = \lg(1\times 2 \times \dots \times n) = \lg 1 + \lg 2 + \dots + \lg n $$
If we take out $\lg 1 + \lg 2 + \dots$ up to but not including $\lg \frac{n}{2}$ from the above series, we have:
$$ \lg \frac{n}{2} + \dots + \lg n \le \lg n! $$
We can also write
$$ \lg \frac{n}{2} + \lg \frac{n}{2} + \dots + \lg \frac{n}{2} \le \frac{n}{2} \times \lg \frac{n}{2} \le \lg n! $$
Therefore $\lg n! \in \Omega(n \lg n)$.
Moreover, we can show $\lg n! \in \Omicron(n \lg n)$ because
$$ \lg n! \le \lg 1 + \lg 2 + \dots + \lg n \le \lg n + \lg n + \dots \lg n \le n \times \lg n $$
So, in fact, $\lg n! \in \Theta(n \lg n)$.
Aside: You can also show this using Stirling's approximation:
$$ n! \approx \sqrt{2\pi n} \left ( \frac{n}{e} \right )^n $$