BST Analysis
- Distinguish between best-case vs. worst-case running time of operations on BST.
The BST provides a reasonably fast implementation of an OrderedSet ADT.
Each of the operations insert, remove, and has (search) start at the root and follow a path down to, in the worst case, the leaf at the lowest level. The time complexity of each operation is, therefore, $\Omicron(h)$ where $h$ is the height of the tree.
The Worst Case
In the worst case, all the nodes in the BST will be arranged in a single path.
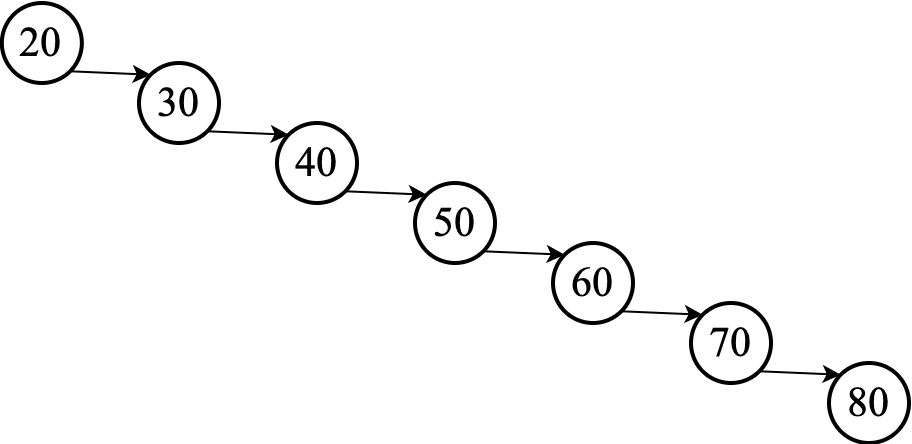
Such a tree would result, for example, from taking a list of $n$ elements in sorted order and inserting them one at a time into an initially empty tree.
The height of a $n$-node tree like the one above is clearly $n - 1$. Therefore, the core operations of OrderedSet ADT will take $\Omicron(n)$ time on a collection of $n$ elements.
The Best Case
In the best case, the BST is a perfect binary tree.
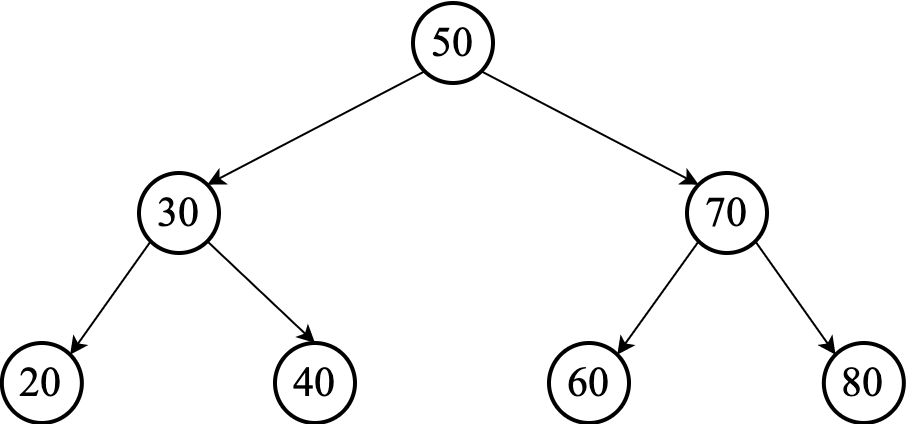
The height of a $n$-node perfect binary tree like the one above is $\Omicron(\lg n)$. Therefore, the core operations of OrderedSet ADT will take $\Omicron(\lg n)$ time on a collection of $n$ elements.
Aside: The average running time is difficult to establish because it is not clear that all BSTs are equally likely, but it has been shown to be similar to the best case. It is beyond the scope of this course to explore the average case.
We will later learn about "Balanced Binary Search Trees" that automatically keep their height within (or close to) $\Omicron(\lg n)$ in the face of arbitrary item insertions and deletions.
Resources
- Binary Search Tree (BST) Worst Case on YouTube.