Merge Sort: Analysis
- Analyze the best and worst-case time efficiency of MergeSort.
The merge sort runs in $\Omicron(n \lg n)$ time.
Justification:
- The number of times the merge sort divides a sequence is the number of times $n$ can be halved: $\Omicron(\lg n)$. Therefore, the divide part has $\Omicron(\lg n)$ levels. At each level $l$, we perform $2^l$ divide (which itself is a constant time). So the total work is $2^0 + 2^1 + \dots + 2^{\lg n} \in \Omicron(n)$.
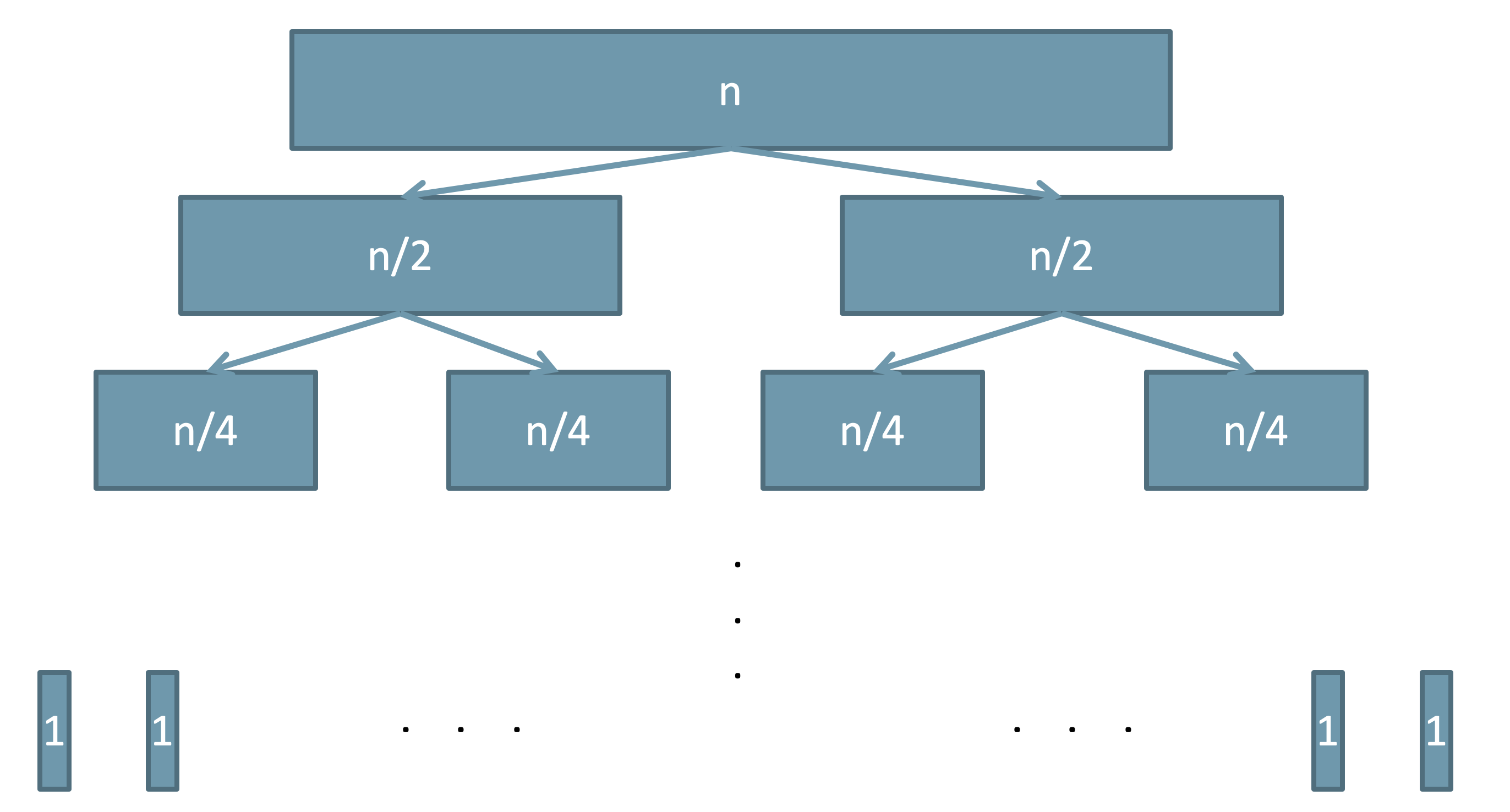
- The number of times merge sort merges the subsequences is equal to the number of sub-sequences. Therefore, the merging part also has $\Omicron(\lg n)$ levels. Consider at each level, we perform $k\times \Omicron(n/k) \in \Omicron(n)$ time to merge the sub-arrays. So the total running time for the merge sort algorithm is $\Omicron(n \lg n)$,
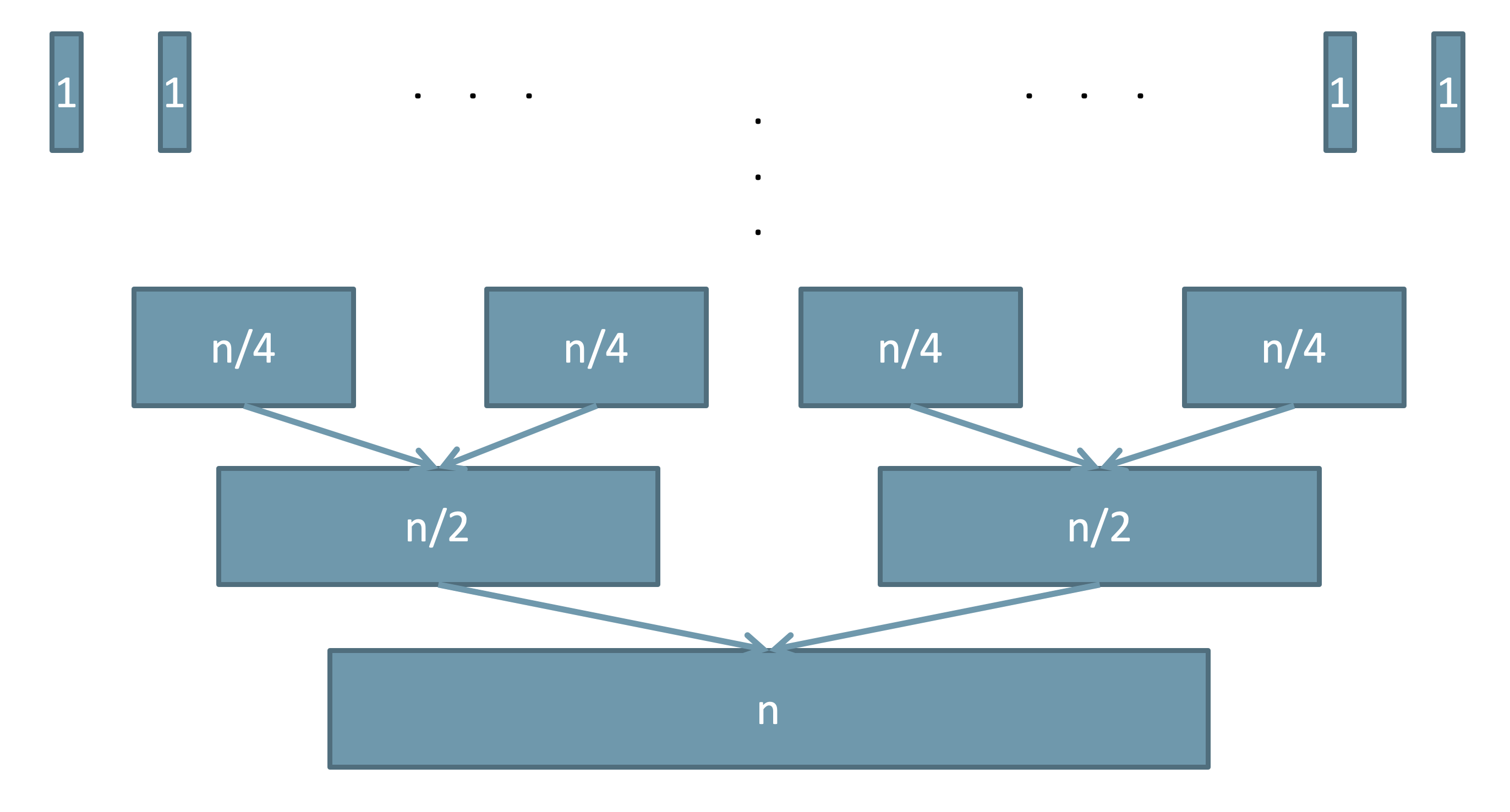
Formal Proof
A formal proof can be constructed by writing the runtime of merge sort as a recurrence relation $T(n) = 2T(n/2) + \theta(n)$ and showing $T(n) \in \theta(n \lg n)$.
If you want to look this up, search for "the master theorem for divide-and-conquer recurrences" and look up "case 2". This is, however, beyond the scope of this course.
Resources
- Analysis of Merge Sort on Khan Academy.
- Wikipedia's entry on Merge sort: Analysis.
- Wikipedia's entry on Master Theorem.