Summary
- Elaborate on the benefits of using asymptotic notation and worst-case analysis to study the computational complexity of algorithms.
The Big-Oh notation and worst-case analysis are tools that greatly simplify our ability to compare the efficiency of algorithms.
- Asymptotic analysis means using asymptotic notation to describe the computational complexity of an algorithm.
- Computational complexity generally means time complexity and space complexity.
- If it is not specified, we mean time complexity.
- If it is not specified, we mean worst-case analysis.
- If it is not specified, we want Big-Oh notation.
- When using Big-Oh, give the tightest upper bound you can find.
- When using big Omega, give the tightest lower bound you can find.
- If it is not specified, space complexity should include input and auxiliary space.
| Notation | Definition |
|---|---|
| $\Omicron$ | Big-Oh: $T(n)$ is a member of $\Omicron(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\le c f(n)$ for all $n\ge n_0$. |
| $\Omega$ | Big Omega: $T(n)$ is a member of $\Omega(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\ge c f(n)$ for all $n\ge n_0$. |
| $\Theta$ | Big Theta: $T(n)$ is a member of $\Theta(f(n))$ if and only if there exist positive constants $c_1$, $c_2$ and $n_0$ such that $c_1 f(n) \le T(n) \le c_2 f(n)$ for $n\ge n_0$. |
The following illustration is taken from the bible of Algorithm, the CLRS book:
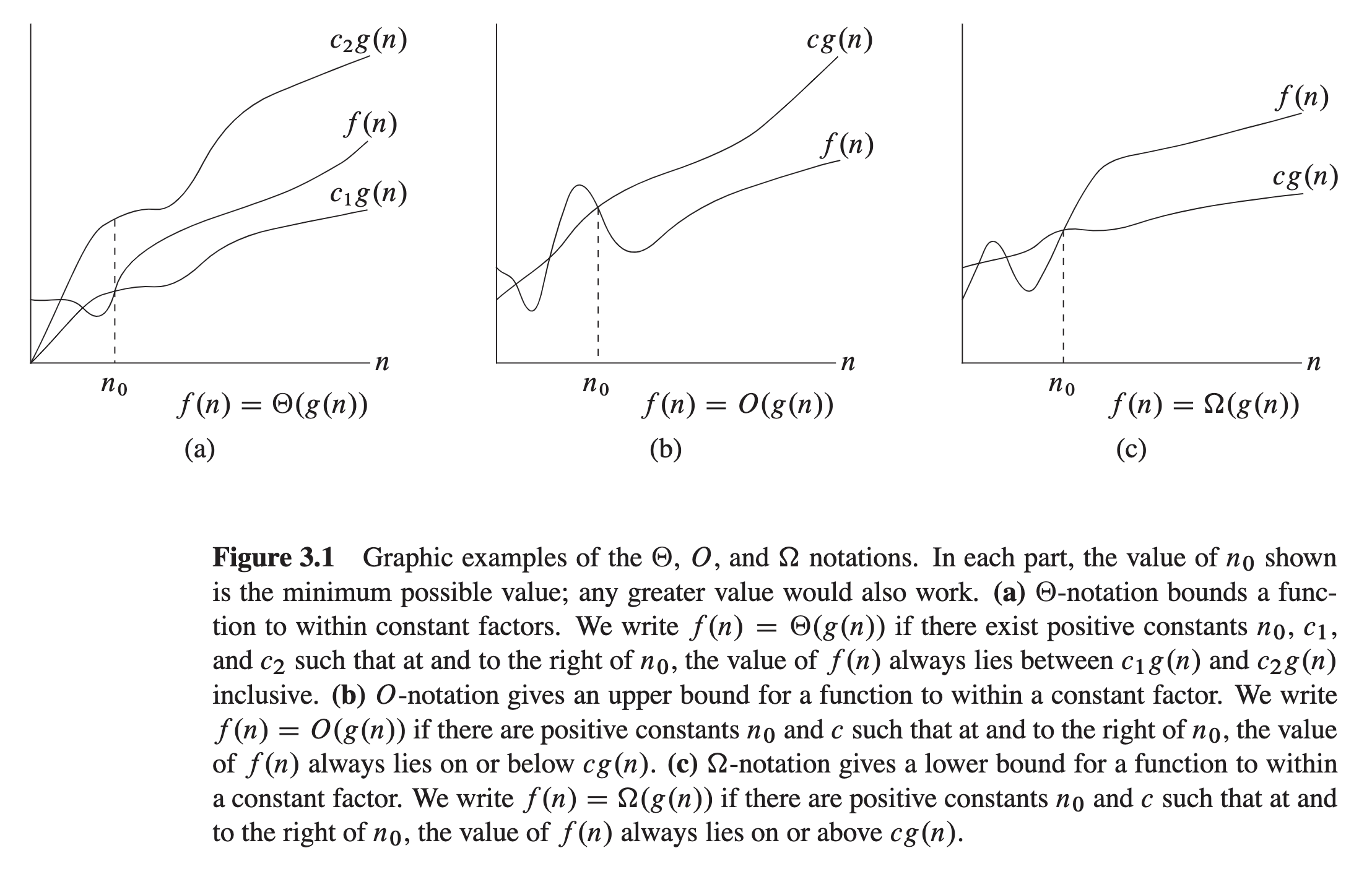
There are other asymptotic notations (Little Oh, Little Omega, etc.) which I have spared you the grief of knowing!
| Notation | Definition |
|---|---|
| $\Omicron$ | Big-Oh: $T(n)$ is a member of $\Omicron(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\le c f(n)$ for all $n\ge n_0$. |
| $\Omega$ | Big Omega: $T(n)$ is a member of $\Omega(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\ge c f(n)$ for all $n\ge n_0$. |
| $\Theta$ | Big Theta: $T(n)$ is a member of $\Theta(f(n))$ if and only if there exist positive constants $c_1$, $c_2$ and $n_0$ such that $c_1 f(n) \le T(n) \le c_2 f(n)$ for $n\ge n_0$. |
Resources
For a brief & concise overview, refer to any of the following:
- Educative's short article on Time complexity vs space complexity
- InterviewCake's article Big-O notation
- HackerEarch's tutorial Time and Space Complexity
- Cornell's cs3110 online lecture notes
- MIT's 16.070 online lecture notes
- Big-O notation in 5 minutes — The basics on YouTube.
- Asymptotic Bounding 101: Big O, Big Omega, & Theta (Deeply Understanding Asymptotic Analysis on YouTube.
- Online notes on Analysis of Algorithms accompanying Robert Sedgewick's book "Algorithms."
- TowardsDataScience's article The Math Behind "Big O" and Other Asymptotic Notations
For an in-depth, detailed, formal (mathematical) discussion of asymptotic analysis, refer to chapter 3, "Growth of Functions," in CLRS: Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein, Introduction to Algorithms. 3rd ed, MIT Press, 2009.