Tree: A Connected Acyclic Graph
- In the context of Graph Theory, define Cycle, Acyclic Graph, and Tree.
A cycle is a path that starts and ends at the same vertex and includes at least one edge.
Another name for a cycle is a "closed path." Having at least one edge means at least two vertices in the path: the start/end and one other.
Consider the following graph:
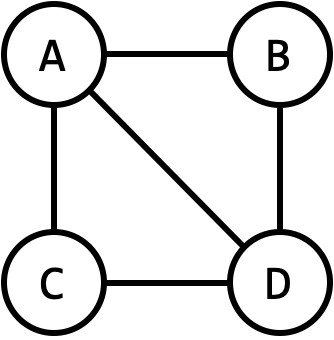
Here is a cycle: $(A, B, D, A)$. Here is another one: $(A, B, D, A, C, D, A)$
A simple cycle is a cycle that includes vertices other than the start/end at most once.
In this class, when I say "cycle," I mean "simple cycle."
Aside: In some references, what I defined as "cycle" is described as "circuit," and instead, "simple cycle" is simply called "cycle."
An acyclic graph is a graph having no cycles.
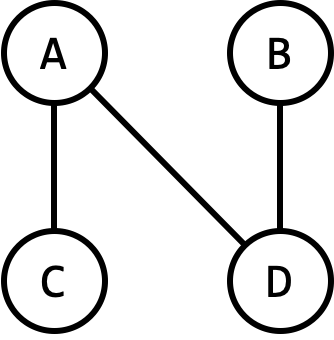
Recall: A graph is called connected if there is a path between every pair of vertices.
A connected acyclic graph is called a tree!
Aside: directed or undirected?
In Mathematics and Graph Theory, trees are assumed to be undirected. However, in the context of Data Structures, a tree is typically rooted (one vertex has been designated as "root") and directed (all edges point away from the root).
Why is a tree considered undirected in Graph Theory? Because a "connected" graph is generally defined as an undirected graph.
In directed graphs, edges connect one node to another, but not necessarily in the opposite direction (the edge relation between vertices is asymmetric). In lieu of this, a directed graph may be weakly connected, unilaterally connected, semi-connected, strongly connected, etc. — the point is that connectivity in directed graph is messy!
Accordingly, the topic covered in this chapter, i.e., minimum spanning tree, is defined for undirected graphs.
It's possible to define MST for directed graphs. Still, it is usually given other names like optimum branching, min-cost arborescence, etc.