Treap: Insertion
- Explain and trace the balancing operations of a Treap.
- Explain the role of the priorities in rebalancing and the importance of being random.
Let's insert the values $1, 2, 3, 4, 5, 6$ into a Treap (in that order).
As you insert each value, assign a random priority to it. For example, below, the priorities are generated from the range $[0, 1]$ and shown under each node.

The insertion process starts as the insertion process of a regular BST, ignoring the priorities. Therefore, the value $2$ goes to the right of $1$.
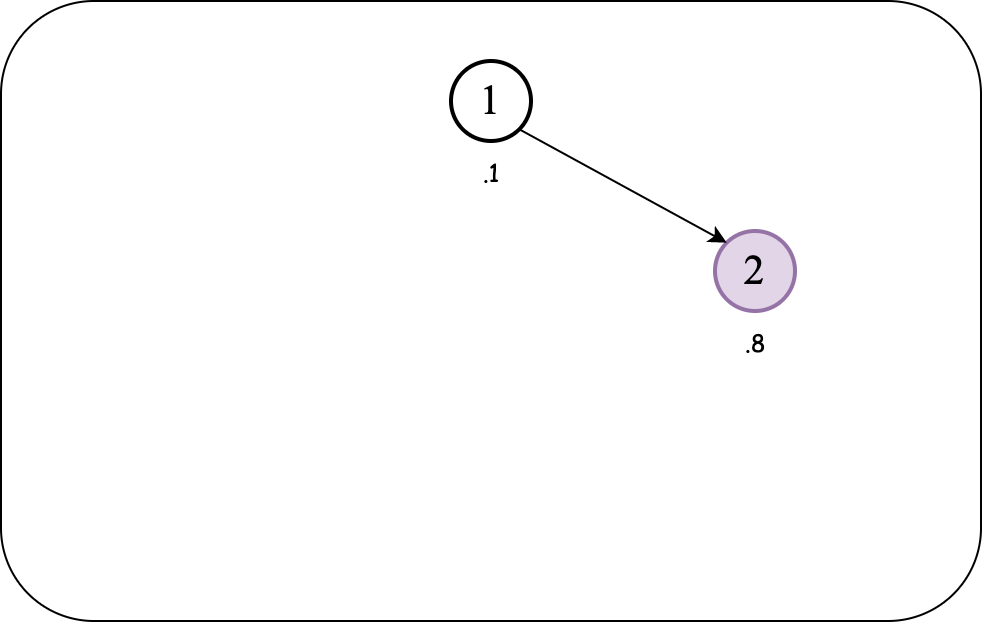
Assuming we maintain a max-heap for this example, the priorities (inserted node and its parent) are not in the desired order. We, therefore, perform a rotate left to bring the node up and parent down.
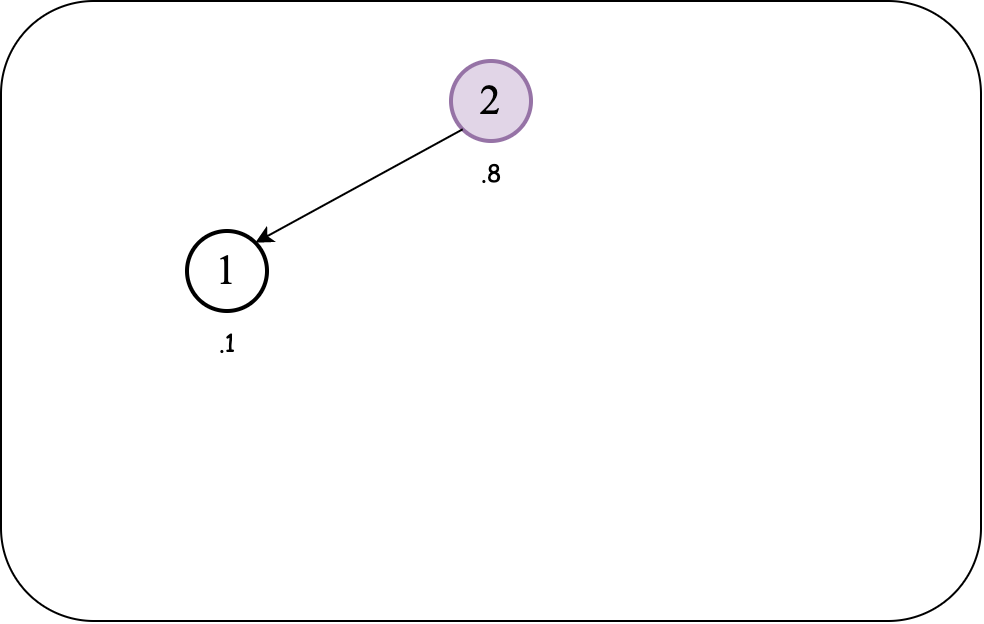
Why we didn't "swip up" the node to replace its parent?
Rotations preserve the BST order property of the keys, but swapping entries (like a heap percolate-up/down) would not!
Let's insert the next value:
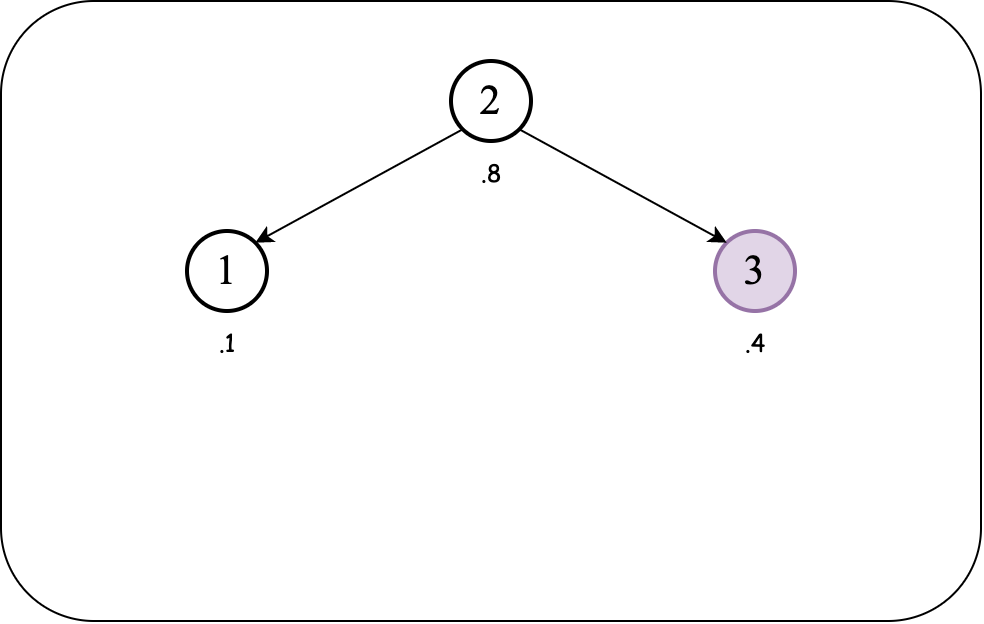
The BST order (over keys) and heap order (over priorities) are maintained. So we insert the next value:
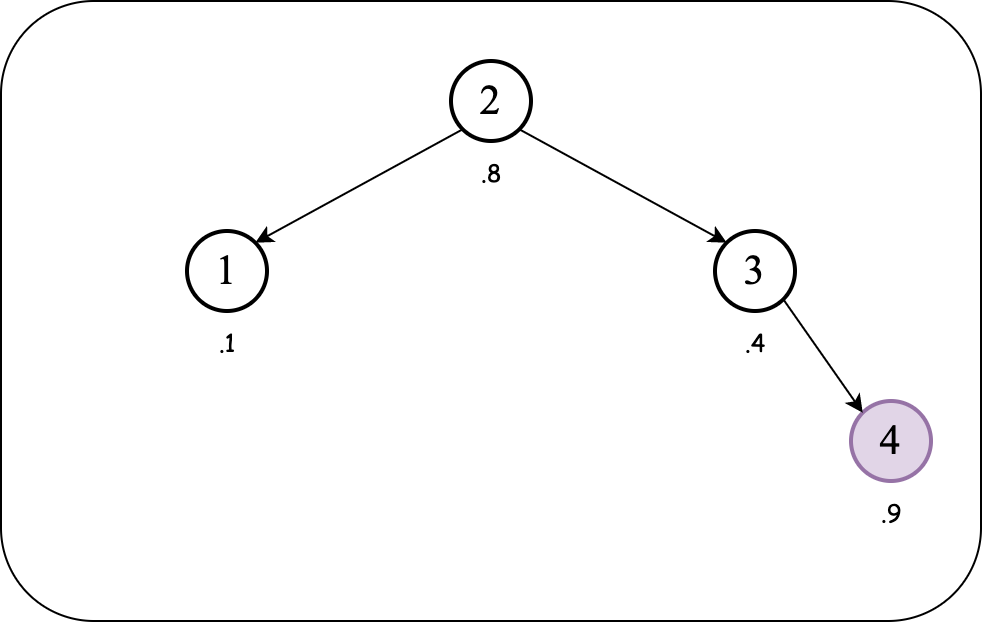
We have a violation of heap order property (over the priorities). So we need to rotate left to bring the inserted node above the parent node to fix the heap order property while maintaining the BST order property.
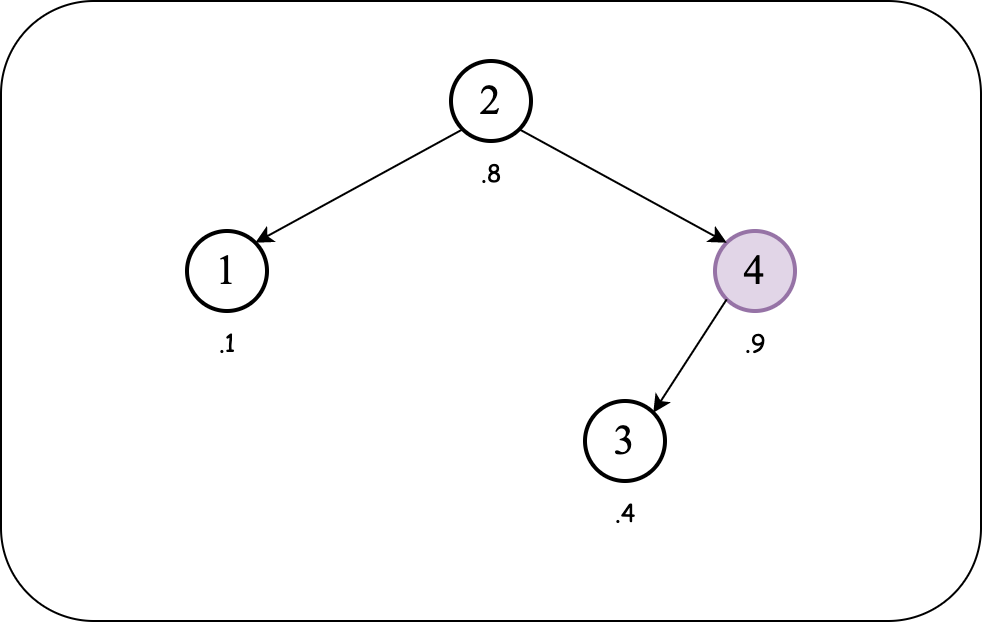
How do we decide to rotate left/right?
If the child node that violates the heap order property is to the parent's right, then you need to rotate left. If the child is to the left of the parent, then you need to rotate right.
We must follow up with another rotate left operation:
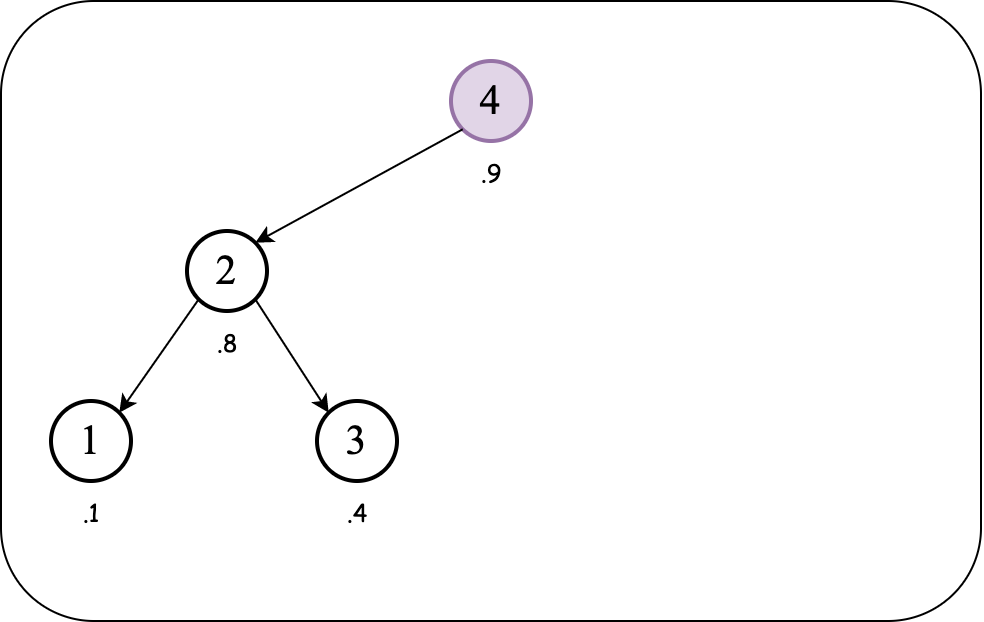
The BST order (over keys) and heap order (over priorities) are maintained. So we insert the next value:
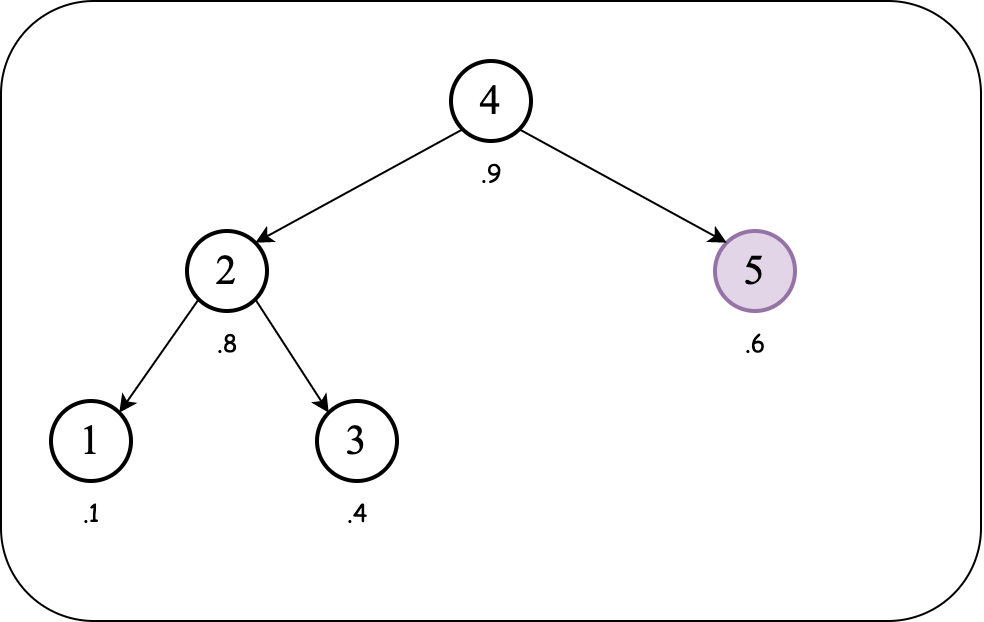
The BST order (over keys) and heap order (over priorities) are maintained. So we insert the next value:
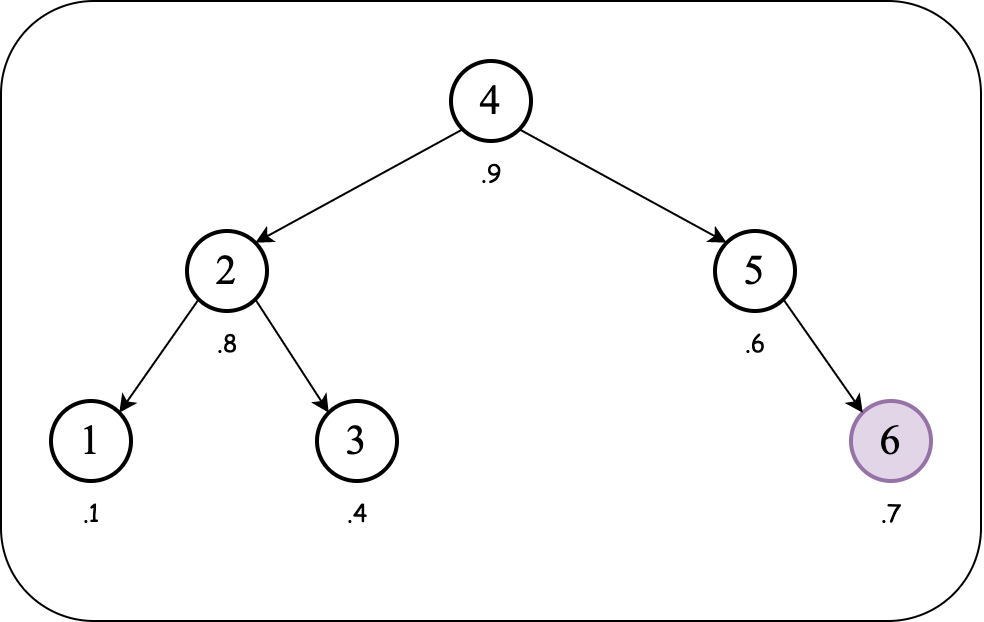
We have a violation of heap order property (over the priorities). Since the inserted (child) node is to the right of its parent, we need to rotate left to bring the inserted node above the parent node.
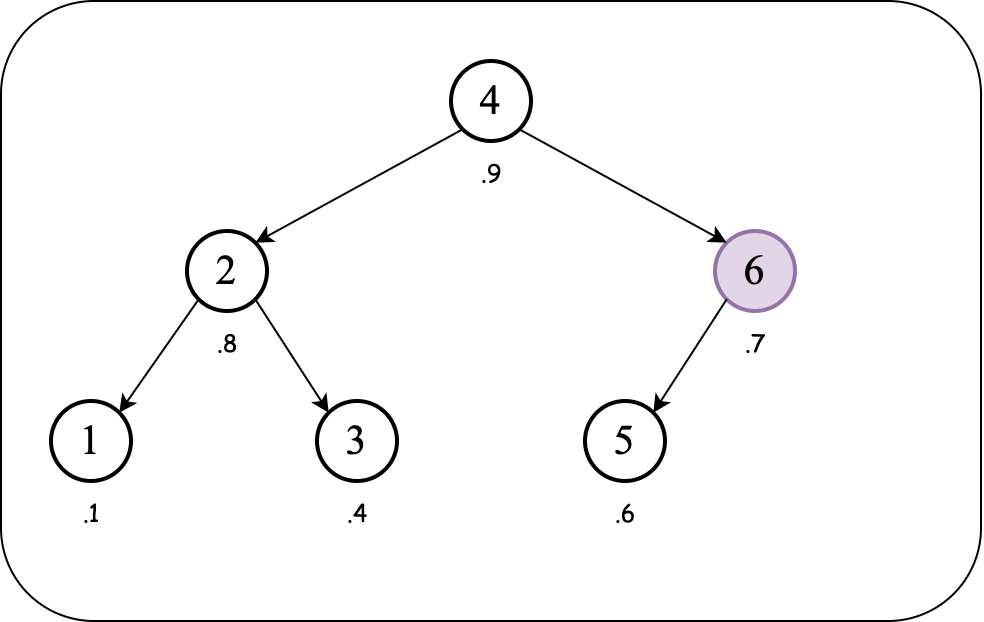
The rotation fixes the heap order property while maintaining the BST order property.
Notice that the resulting BST is balanced even though we inserted $1$ to $6$ in sorted order.